Proposal: Conveyor performance - code optimization design

As a computer programmer, conveyor system tickles me a lot for some reason. There was a question that didn't let me sleep. If you have a conveyor system, where only two cargo containers exist, yet any amount of conveyors. What is the complexity of pushing resources from one cargo? Obviously, there is only one other cargo container, so only one possible result exists. Shouldn't be the complexity same for any amount of conveyors then?

For a while I have been going around questioning people with this, but I was not getting satisfying answers. Many claimed conveyors are important and lot more myths. Since in my tests long network with 2 cargos behaves differently from short networks with 2 cargos, I belived rummors can be true and this could be optimized. So I have tried to design solution myself.

First idea I had was simple. I need to optimize the conveyor network before resource transfers. Create a shadow network in behind. That way I will relief some complexity. Block with inventories seems to be only important. Why not to just remember distances for each inventory block in the network?

So I assigned array to each intentory block and fill it with other inventory block references sorted by distance.

This was first and simple shadow network. But it had a fatal flaw. Used memory was close to n^2 and with growing amount of cargos, it was impossible to bear.

I realized I will need to keep the amount of pointers to constant amount. Then another idea emerged. The entire network is basically linked list. With limited amount of pointers. The problem is, some nodes has no impact on results. Yet have impact on complexity since they need to be iterated.

There my dark days started. Logic seemed to be correct, but I couldn't develop a simple way of optimizations. Each time I had something new I also found an example that didn't fit in. Took me long time. But eventually I did not give up.

I started to do some serious diagrams and drawings. That speeded me up. I reallized once network is mapped, it's position in 3d space is not important at all. The only important factor are pointers. Each pointer by default has lenght of 1, because its neighbour is just next to it. And in 3d space, each block has maximum of 6 pointers to its neighbours. I reallized I might not want to change this factor.

For greater simplicity I made my diagrams only in 2d space (reducing neighbours to 4). And reallizing principles might be same.

I find out, that some nodes can be removed. For example those that has exactly 2 neighbours can be spliced, while lenght increased by 1.

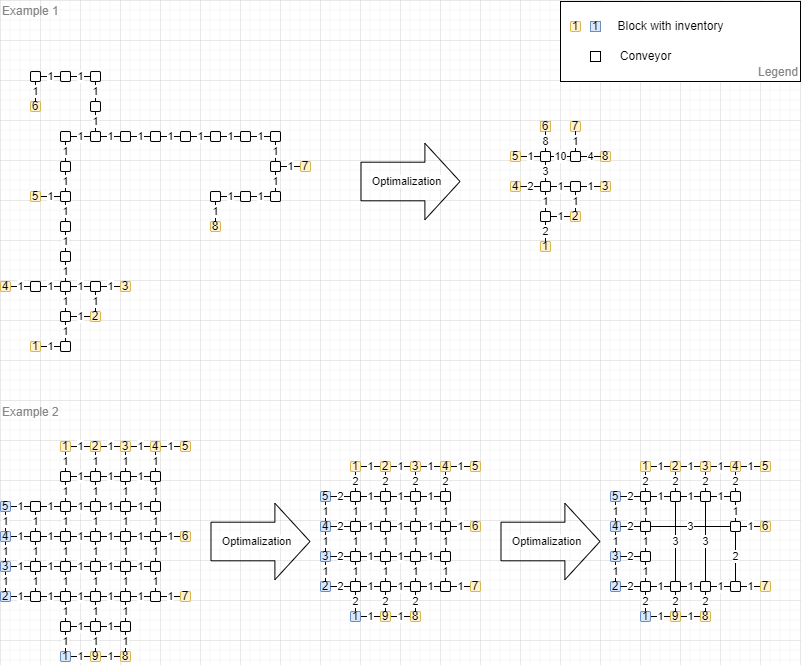
After short work and repeating few operations, I have managed to simplify quite complex networks in much smaller versions as diagram shows. What is important distance from any inventory block to any other inventory block remains the same, but requires less iterations in most cases.

For the pathfinding, modified version of Dijkstra's algorithm can be used and we are done here.

Now I have found some significant positives of this approach I would like to share.

Low complexity of simplification methods

As I mentioned one of the simplest operation is just remove conveyors, that has 2 connections only. Such a operation is quite cheap to cast on the entire network.

Step by step simplification

What we start with is some conveyor network that is difficult for pathfinding. When one simplification operation is applied, you end up with conveyor network with same distances, but less nodes. Thus you can already use this for resource traveling. You do not have to do entire simplification proccess in one tick/frame/step, yet you can benefit from its results immidiately after each operation.

Network doesn't have to be a master piece

There are different operation that can be casted to make network simple. Yet not all of them has to be implemented to make this work. Even one operation type will make system more efficient.

Local updates only

In case the network is extended with new block or reduced, recalculations have to be done. But new operations can happen only in local sector. System doesn't need to recalculate the entire network.

Almost any network can be simplified

I belive this can simplify almost every network and reduce the amount of conveyors by 50%-100%. Simplification is basicaly given by amount of inventory blocks in the network. Remaining amount of conveyors exists ony to keep amount of pointers linear. One of the worst examples would be probably chess pattern of cargos and conveyors. But I think even that one could be reduced.

Just writting this down took me 3 hours. And research itself, I have lost count. It would be nice if somebody replied literally anything :)

Sources for this research & knowledge:

Testing conveyors in private game, using debug

Diagrams you can play with: https://drive.google.com/file/d/1zDZ50ZBYKCd1pNDeXM-jB7TcjuTTFn4z/view?usp=sharing & https://diagrams.net/

Linked list: https://en.wikipedia.org/wiki/Linked_list

Dijkstra's algorithm: https://www.youtube.com/watch?v=GazC3A4OQTE

Cellular automata & game of life: https://natureofcode.com/book/chapter-7-cellular-automata/

More tests of conveyors: https://www.youtube.com/watch?v=6VWj4sx2aqk